
数学a 整数 約数 等式を満たす整数x Yの組の解き方を簡単に解説 都立高校受験応援ブログ
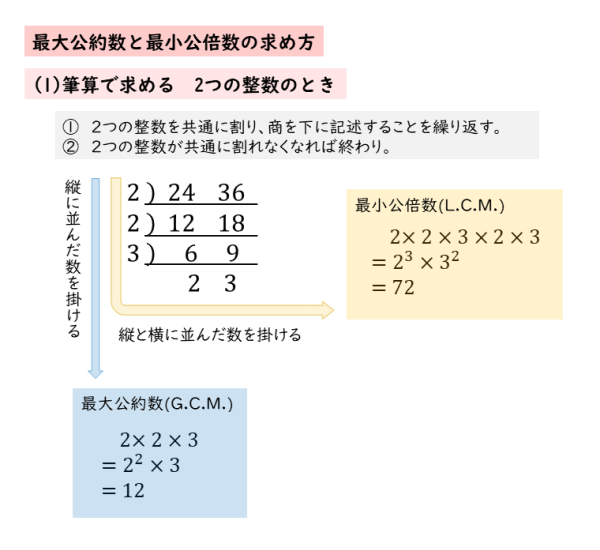
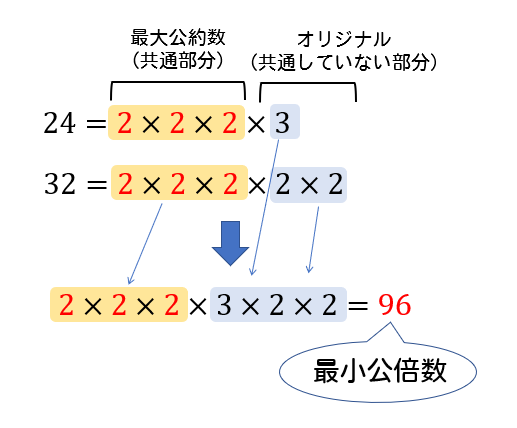
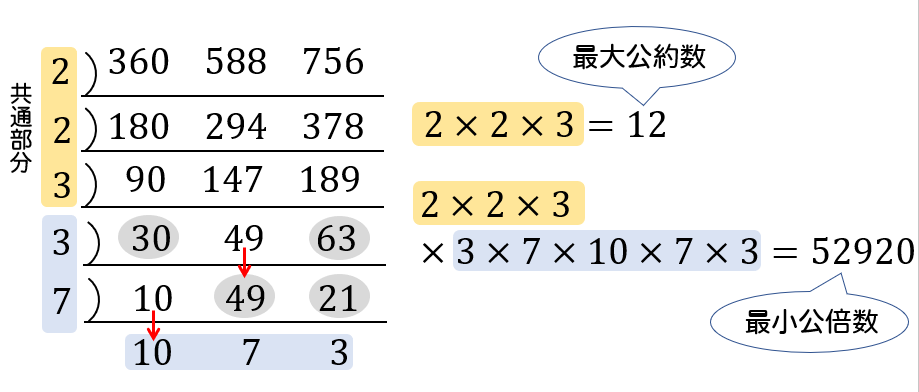
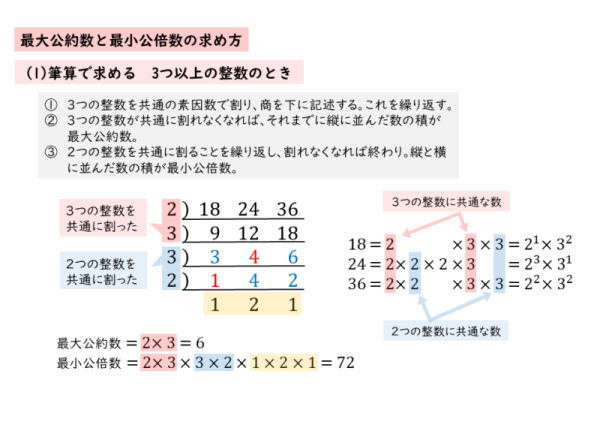
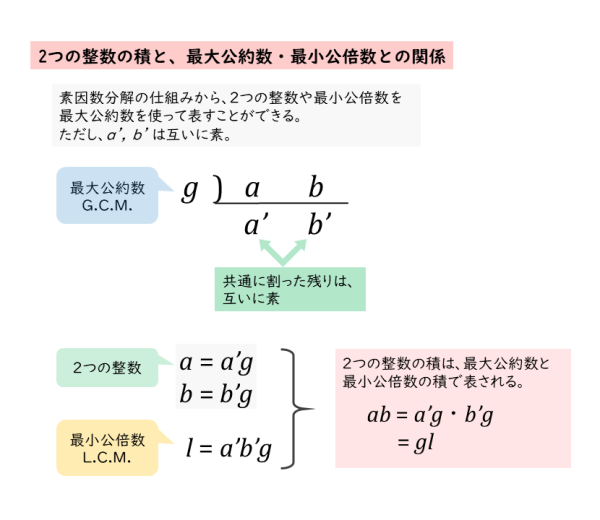
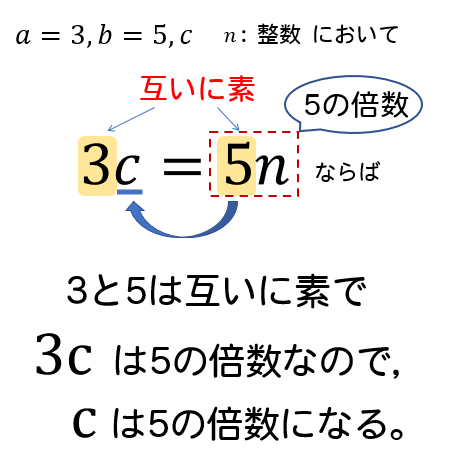
約数と倍数 a,b,k a, b, k を整数とする。 a = bk a = b k という関係が成り立つとき, a a は b b の倍数といい, b b は a a の約数という。 2個以上の整数に共通の約数を公約数といい,その中で最大のものを最大公約数という。 また,2個以上の整数に共通の倍数を公倍数といい,その中で最小のものを最小公倍数という。 ホーム 定理・公式・証明高校数学 計算するときに意外と役に立つのが、 倍数の判定法 です。 割り切れるかどうかが分かるということは、 倍数や約数の関係を見抜ける ということです。このような知識を持っていると、分数を扱う機会が増える高校数学では重宝します。
約数と倍数 高校
約数と倍数 高校- You're signed out Videos you watch may be added to the TV's watch history and influence TV recommendations To avoid this, cancel and sign in to on your computer Cancel Confirm Switch複数の整数の最大公約数と最小公倍数について 目次 1.複数の整数の最大公約数と最小公倍数を考える意義 2.基本用語の復習 2-1.約数と倍数の復習 2-2.公約数と公倍数の復習 2-3.最

中学数学より4 教科書に登場しない最小公倍数 最大公約数 身勝手な主張
約数と倍数 (整数の性質)|高校数学のつまずきやすい単元を徹底解説! 数学が苦手なお子さんの数は中学、高校とも学年が上がっていくごとに増えていきますよね。 特に中学から高校に上がって高校1年生から分からなくなってしまう人が多いです。 今回は高校1年生の数学の中でも約数と倍数について書いていきたいと思います。 「約数と倍数」のような整数の 最後に 1 − 4 3 = 0 143=0 1− 43 = 0 となり11の倍数の判定法がヒットする: 858 = 2 × 3 × 11 × 13 858=2\times 3\times 11\times 13 858 = 2× 3×11 ×13 このように倍数の判定法が続々とヒットすればラッキーですが, 47 = 23 × 47=23\times 47 = 23× のように倍数の判定法がヒットしない合成数は素因数分解するのが大変ですね( 47 約数と倍数 二つの整数 について、 が で割り切れるとき、 は の約数、 は の倍数であるといいます。 例えば、 と という二つの整数について、 は で割り切れるので、 は の約数であり、 は の倍数であるということとなります。
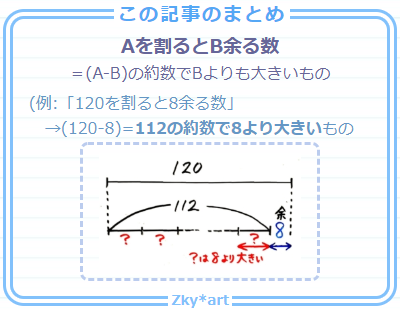
基本編(約数、公倍数公約数)の実践編です。 (1)約数の数が3個あり、約数を全て足すと463になる自然数を求めなさい。 (2)504の約数の中で、4の倍数である約数の総和を求めなさい。 (3)150の約数の逆数の和と2約数と倍数〈1P〉高校数学教科書レベル ご視聴いただきありがとうございました! コメントを書いていただけると励みになりますの 基本編 (約数、公倍数公約数) の実践編です。 (1)約数の数が3個あり、約数を全て足すと463になる自然数を求めなさい。 (2)504の約数の中で、4の倍数である約数の総和を求めなさい。 (3)150の約数の逆数の和と2乗した数の和を求めなさい。 (4)最大公約数が12で最小公倍数が144である2つの自然数の組み合わせは全部で何組あるか。 (5)最小公倍数が640で和が74で
約数と倍数 高校のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  | |
 |  | |
「約数と倍数 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「約数と倍数 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「約数と倍数 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「約数と倍数 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「約数と倍数 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「約数と倍数 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「約数と倍数 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「約数と倍数 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「約数と倍数 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「約数と倍数 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「約数と倍数 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |
約数と倍数 定義 2つの整数 a a , b b について,ある整数 k k を用いて a = bk a = b k と表されるとき, b b は a a の 約数 であるといい, a a は b b の 倍数 であるという。 a = bk a = b k のとき, a = (−b) ⋅(−k) a = ( − b) ⋅ ( − k) でもあるから, b b が a a の約数ならば −b − b も a a の約数である。 スポンサーリンク24=1×24=2×12=3×8 24を2つの自然数のかけ算の形で表していくと、次のようになるよ。 「1とかけ算して24になるのは24、2とかけ算して24になるのは」と順に考えていくと、「1×24」「2×12」「3×8」「4×6」が見つかるね。 これらの数字がすべて24の約数になる んだ。 「4×6」 の後を考えると 「6×4」 が出てくるけど、これは「4×6」と同じこと。 折り返し地点 が
Incoming Term: 約数と倍数 高校,




0 件のコメント:
コメントを投稿