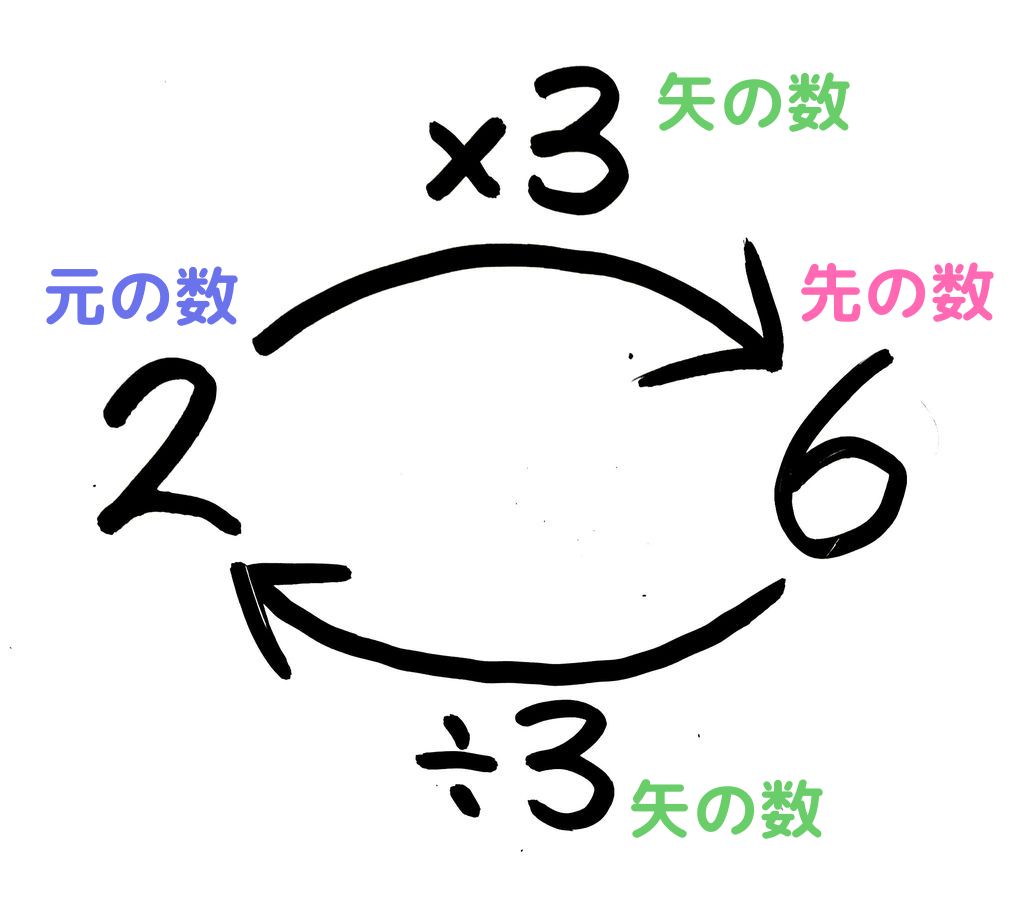
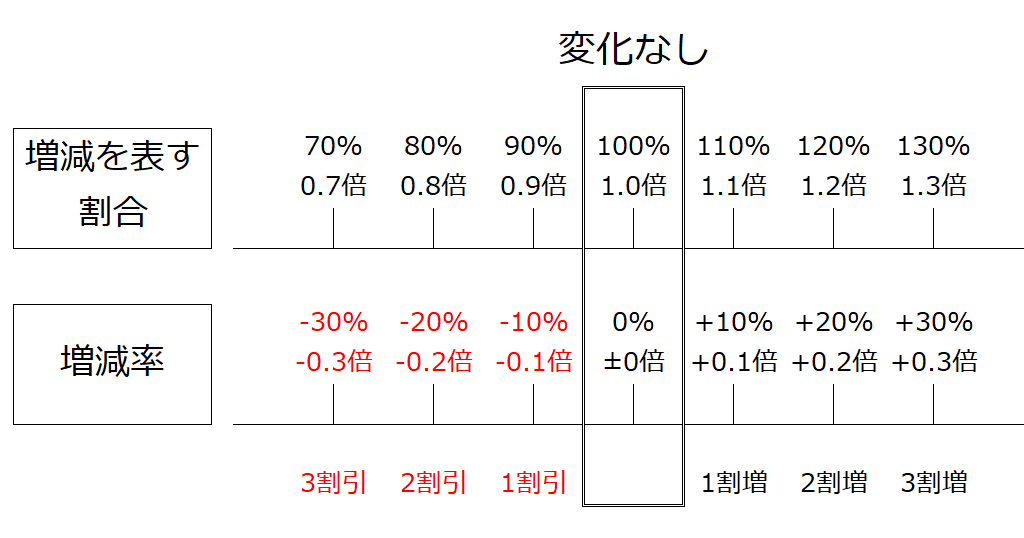
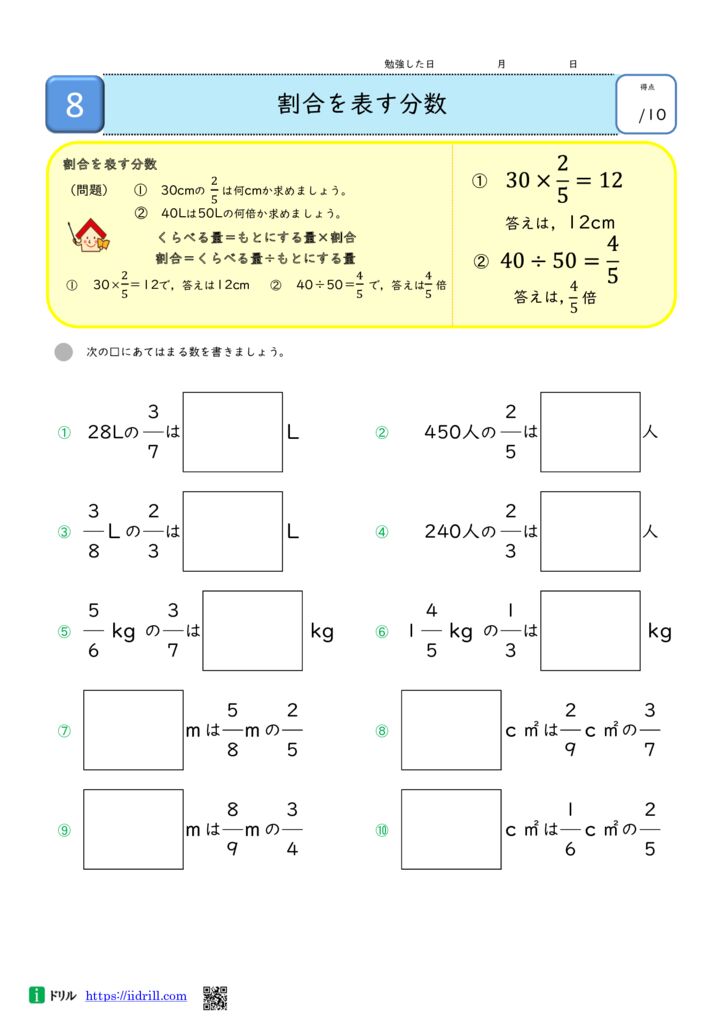
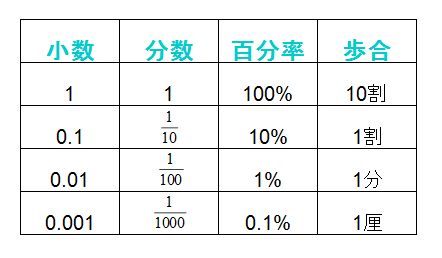
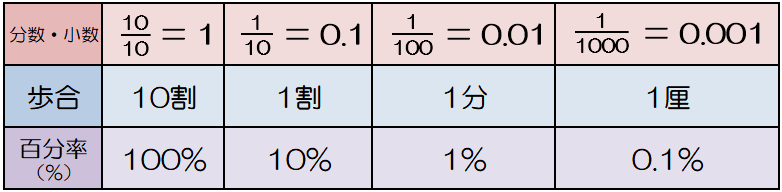
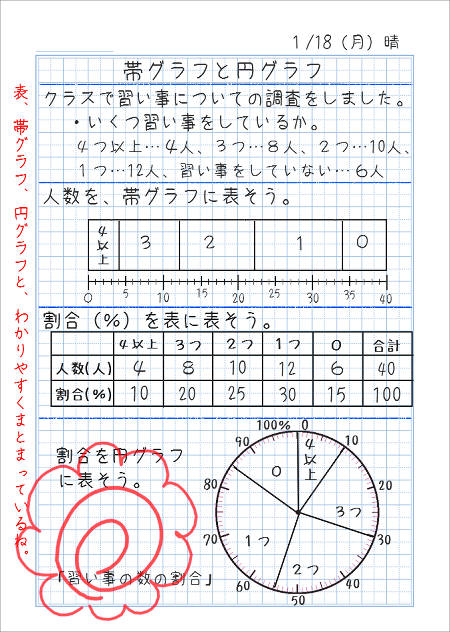
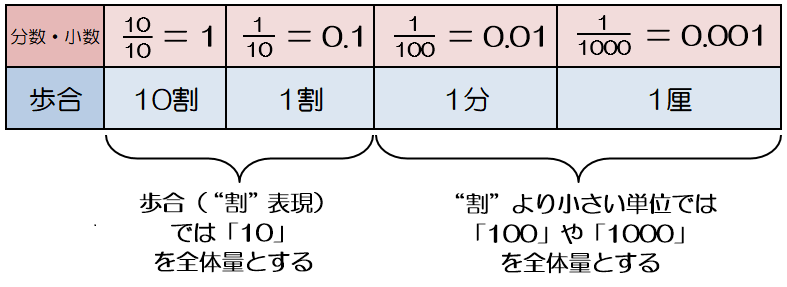
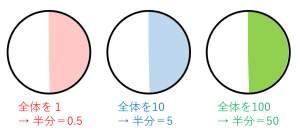
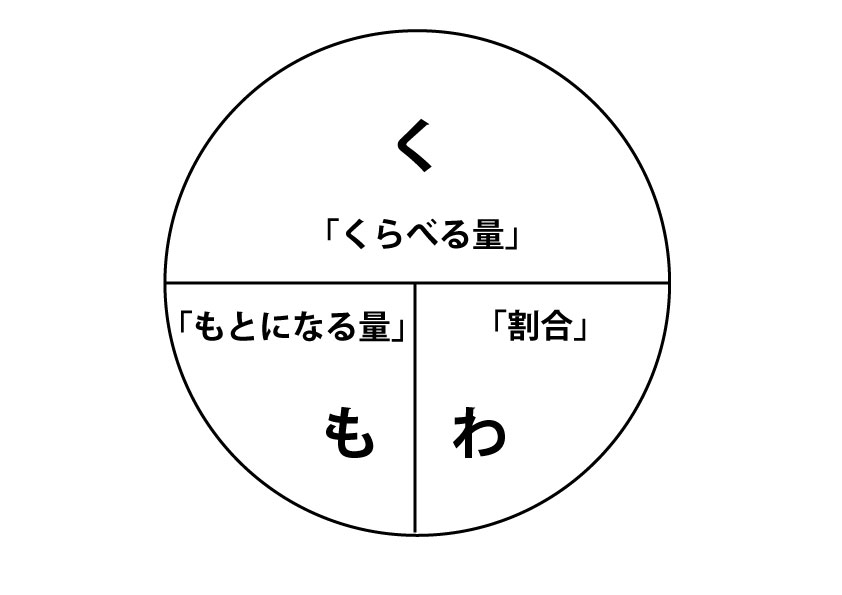
割合は「くらべる数」を「もとの数」で割った $$ 割合 = \frac{くらべる数}{もとの数} $$ で計算することができます。 百分率(%)は、001 を 1% とするとので $$ 百分率 = 割合 \times 100 $$ で計算できます。 これらの関係を使って、次の計算をしてみましょう。
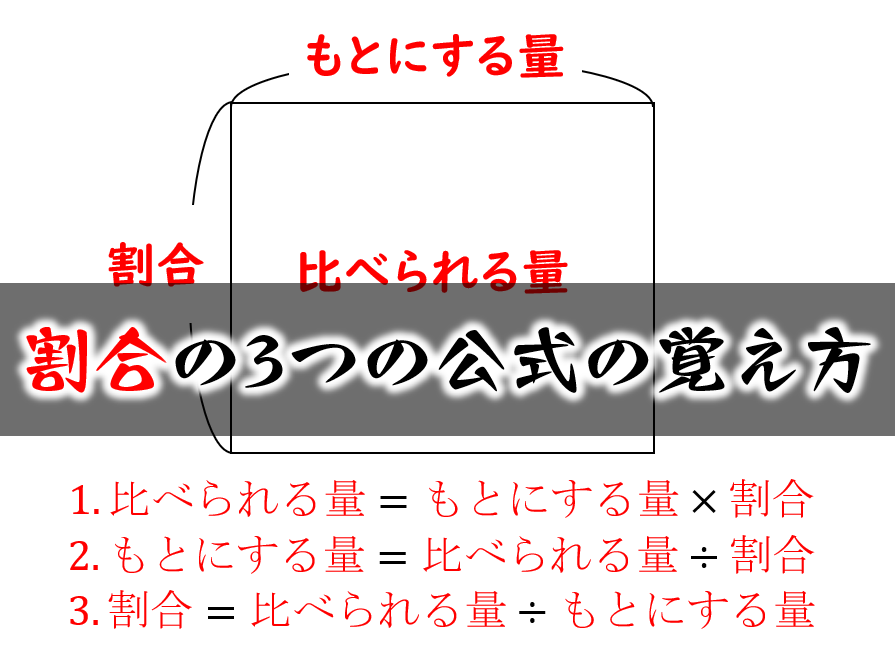
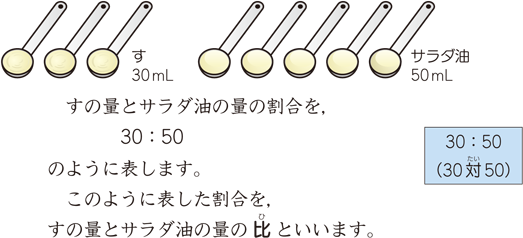
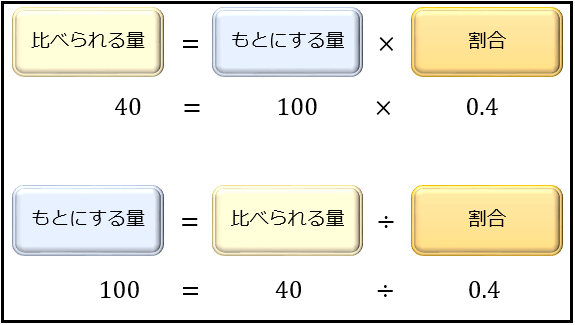
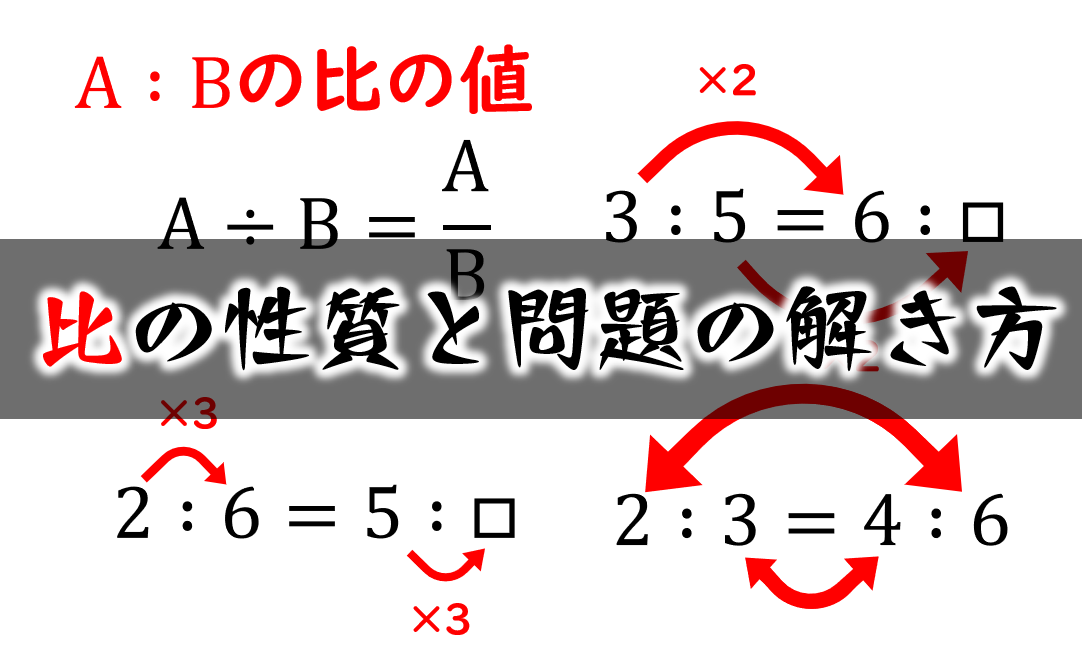
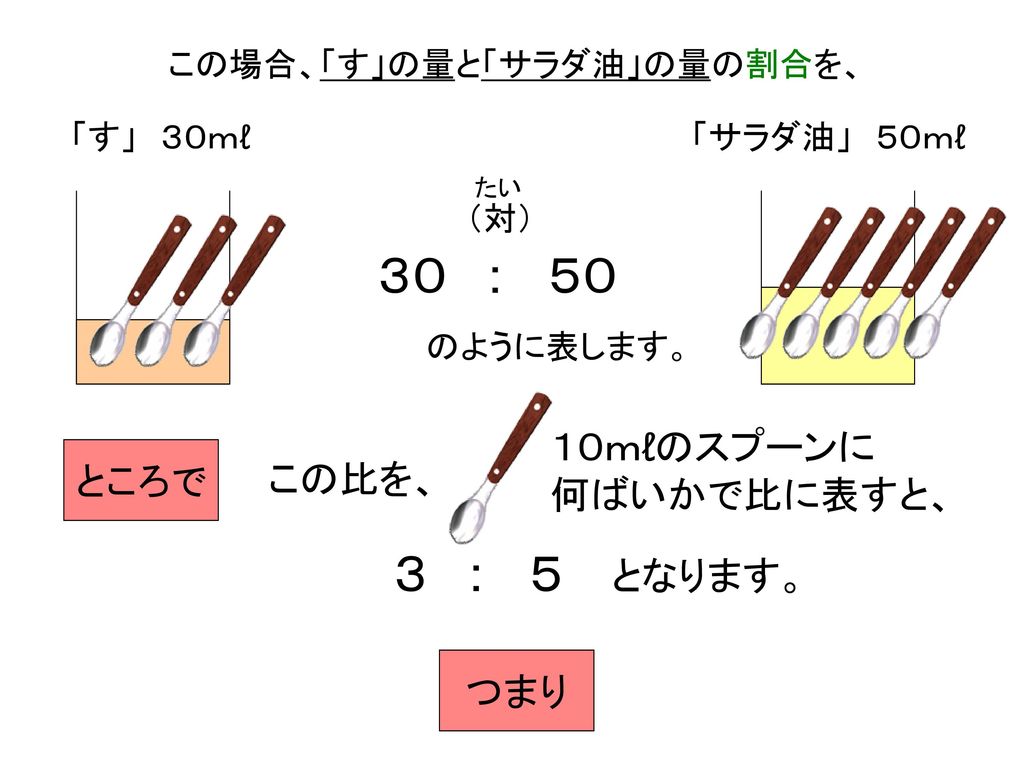
割合の表し方を考えよう 小田- 割合とは、 「比べられる量」を「もとにする量」 で割ることで求められる値です。 割合は 「比べられる量」が「もとにする量」の何倍なのか を表しています。 例えば、割合が 04 とは「比べられる量 ( 40 )」が「もとにする量 ( 100 )」の 04 倍であるということを意味します。 「割合」=「比べられる量」÷「もとにする量」 「比べられる量」=「もとに料理で使うだしの比の使い方 だしの商品の説明書き 実物を見せて、「比」が日常生活に 役立っていることを教えます。 教え方1 お酢とサラダ油を混ぜて、ドレッシングを作り、その割合の表し方を通して、比の意味をとらえさせます。
割合の表し方を考えよう 小田のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  |  |
 |  | |
 |  |  |
「割合の表し方を考えよう 小田」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  |  |
 |  |  |
「割合の表し方を考えよう 小田」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  | |
「割合の表し方を考えよう 小田」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 | ||
 |  |  |
「割合の表し方を考えよう 小田」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 | ||
「割合の表し方を考えよう 小田」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
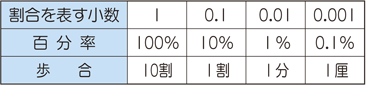 |  | |
 |  | |
「割合の表し方を考えよう 小田」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 | ||
「割合の表し方を考えよう 小田」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
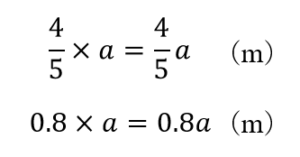 | ||
「割合の表し方を考えよう 小田」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |
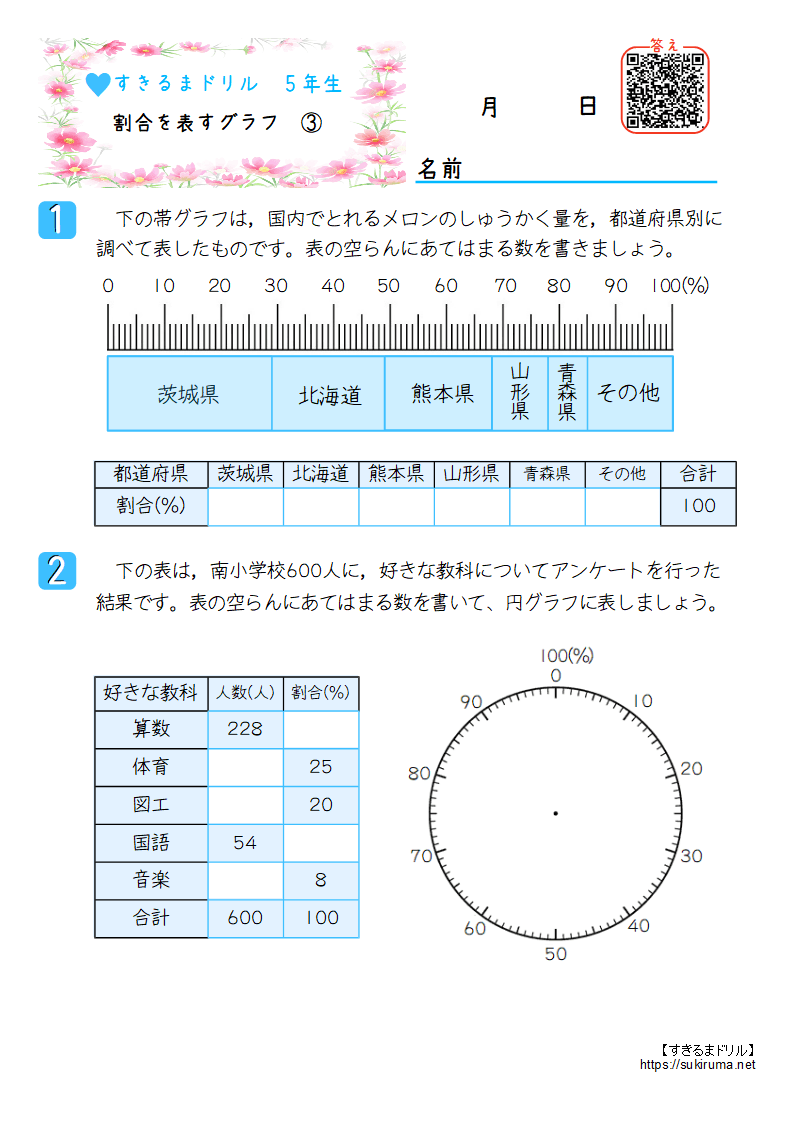
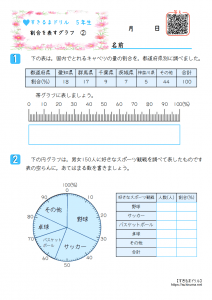
最終的な 食塩水の量は 250 g ( 元の食塩水 0 g + 加えた水 50 g )で、 食塩の量が 30 g なので、 この時の割合 を求めます。 「 比べられる量 」÷「 元にする量 」=「 割合 」を使い、30 ÷ 250 = 012 よって割合は「 12 % 」となります。割合の問題を苦手にしている生徒さんは多いです。 しかし、ポイントは2つです。 1どの割合の問題が上記で扱った割合の3パターンのどの問題にあてはまるか判断する 2判断したら、その3パターンの割合の問題を数式に表し、下記にあげた3パターンで解く。
Incoming Term: 割合の表し方を調べよう, 割合の表し方を調べよう 指導案, 割合の表し方, 割合の表し方を考えよう, 割合の表し方を調べよう 導入, 割合の表し方を考えよう 指導案, 割合の表し方 6年 研究授業, 割合の表し方 英語, 割合の表し方を考えよう 小田,




0 件のコメント:
コメントを投稿